Calculation of heating radiators: how to calculate the required number and power of batteries
A well-arranged heating system will provide housing with the necessary temperature and will be comfortable in all rooms in any weather. But in order to transfer heat to the airspace of residential premises, you need to know the required number of batteries, right?
To find out this will help the calculation of heating radiators, based on calculations of the thermal power required from the installed heating devices.
Have you ever done such calculations and are afraid to make a mistake? We will help to deal with the formulas - the article considers a detailed calculation algorithm, analyzes the values of individual coefficients used in the calculation process.
To make it easier for you to understand the intricacies of the calculation, we have selected thematic photo materials and useful videos explaining the principle of calculating the power of heating devices.
The content of the article:
- Simplified calculation of heat loss compensation
- Detailed formula for calculating thermal power
- Orientation of rooms to the cardinal points
- Taking into account the influence of external walls
- The dependence of radiators on thermal insulation
- Climate is an important factor in arithmetic
- Features calculation of high rooms
- The estimated role of the ceiling and floor
- Frame quality is the key to heat
- Window size matters
- The effect of battery closure
- Radiator Connectivity
- A practical example of calculating thermal power
- Specific thermal power of battery sections
- Calculation of the number of sections of radiators
- Improving heat transfer efficiency
- Conclusions and useful video on the topic
Simplified calculation of heat loss compensation
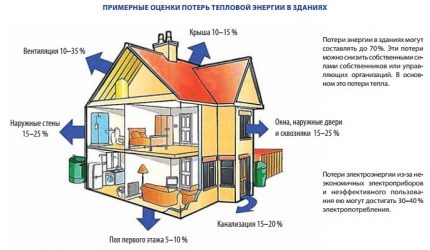
Any calculations are based on certain principles. The calculation of the required thermal power of the batteries is based on the understanding that well-functioning heating devices must fully compensate for the heat loss that occurs during their operation due to the characteristics of the heated rooms.
For living rooms located in a well-insulated house, located, in turn, in a temperate climate zone, in some cases a simplified calculation of compensation for heat leaks is suitable.
For such rooms, the calculations are based on a standard power of 41 W, which is required for heating 1 cubic meter. living space.
The formula for determining the heat output of radiators necessary to maintain optimal living conditions in a room is as follows:
Q = 41 x V,
Where V - the volume of the heated room in cubic meters.
The obtained four-digit result can be expressed in kilowatts, reducing it at the rate of 1 kW = 1000 watts.
Detailed formula for calculating thermal power
In detailed calculations of the number and size of heating batteries, it is customary to start from a relative power of 100 W, which is necessary for normal heating of 1 m² of a certain standard room.
The formula for determining the heat output required from heating appliances is as follows:
Q = (100 x S) x R x K x U x T x H x W x G x X x Y x Z
Factor S in calculations, it’s nothing but the area of a heated room, expressed in square meters.
The remaining letters are various correction factors, without which the calculation will be limited.

But even additional design parameters can not always reflect the specifics of a room. In case of doubt in the calculations, it is recommended to give preference to indicators with large values.
It’s easier then to lower the temperature of the radiators with temperature control devicesthan freezing with a lack of thermal power.
Next, each of the coefficients involved in the calculation of the thermal power of the batteries is analyzed in detail.
At the end of the article, information is given on the characteristics of collapsible radiators from different materials, and the procedure for calculating the required number of sections and the batteries themselves is examined based on the basic calculation.
Orientation of rooms to the cardinal points
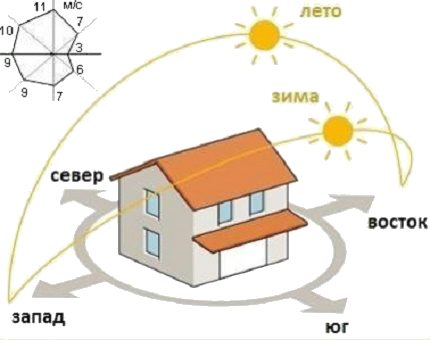
And on the coldest days, the energy of the sun still affects the thermal balance inside the home.
On the direction of the rooms in one direction or another, the coefficient “R” of the formula for calculating thermal power depends.
- Room with a window to the south - R = 1,0. During daylight hours, it will receive maximum additional external heat compared to other rooms. This orientation is taken as the base, and the additional parameter in this case is minimal.
- The window faces west - R = 1,0 orR = 1.05 (for areas with a short winter day). This room will also have time to get its portion of sunlight.The sun, though, will glance there in the late afternoon, but still the location of such a room is more advantageous than the eastern and northern ones.
- The room is oriented to the east - R = 1,1. The rising winter luminary is unlikely to have time to properly heat such a room from the outside. For battery power, extra watts will be required. Accordingly, we add to the calculation a tangible correction of 10%.
- Outside the window is only the north - R = 1,1 or R = 1.15 (a resident of the northern latitudes will not be mistaken, who will take an additional 15%). In winter, such a room does not see direct sunlight at all. Therefore, it is recommended that the calculations of the thermal return required from radiators be also adjusted by 10% upwards.
If winds of a certain direction prevail in the area of residence, it is advisable for rooms with windward sides to increase R up to 20% depending on the strength of the blow (x1.1 ÷ 1.2), and for rooms with walls parallel to cold flows, raise the value of R by 10% (x1.1).
Taking into account the influence of external walls
In addition to the wall with a window or windows built into it, other walls of the room may also have contact with the outside cold.
The external walls of the room determine the coefficient "K" of the calculated formula for the thermal power of radiators:
- The presence of one street wall in a room is a typical case. Everything is simple with the coefficient - K = 1,0.
- Two external walls will require 20% more heat to heat the room - K = 1,2.
- Each subsequent outer wall adds 10% of the required heat transfer to the calculations. For three street walls - K = 1.3.
- The presence of four external walls in the room also adds 10% - K = 1.4.
Depending on the characteristics of the room for which the calculation is carried out, it is necessary to take the appropriate coefficient.
The dependence of radiators on thermal insulation
To reduce the budget for heating the internal space allows competently and reliably isolated from the winter cold housing, and significantly.
The degree of insulation of street walls obeys the coefficient "U", which reduces or increases the estimated thermal power of heating devices:
- U = 1,0 - for standard external walls.
- U = 0.85 - if the insulation of street walls was carried out according to a special calculation.
- U = 1.27 - if the external walls are not sufficiently cold-resistant.
Walls made of climate-friendly materials and thickness are considered standard. As well as reduced thickness, but with a plastered outer surface or with a surface external thermal insulation.
If the area permits, then it is possible to produceinsulating walls from the inside. And to protect the walls from the cold outside there is always a way.

Climate is an important factor in arithmetic
Different climatic zones have different indicators of minimally low street temperatures.
When calculating the heat transfer power of radiators, the coefficient “T” is provided for taking into account temperature differences.
Consider the values of this coefficient for various climatic conditions:
- T = 1.0 to -20 ° C.
- T = 0.9 for winters with frost up to -15 ° С
- T = 0.7 - up to -10 ° С.
- T = 1,1 for frosts up to -25 ° C,
- T = 1.3 - to -35 ° C,
- T = 1.5 - below -35 ° C.
As you can see from the list above, winter weather to -20 ° C is considered normal. For areas with such the least cold take a value of 1.
For warmer regions, this calculated coefficient will lower the overall calculation result. But for areas of harsh climate, the amount of heat required from heating appliances will increase.
Features calculation of high rooms
It is clear that out of two rooms with the same area, more heat will be required for the one with a higher ceiling.To take into account the correction for the volume of heated space in the calculations of the thermal power, the “H” coefficient helps.
At the beginning of the article, a certain normative premise was mentioned. Such is considered a room with a ceiling at a level of 2.7 meters and below. For her, take the value of the coefficient equal to 1.
Consider the dependence of the coefficient N on the height of the ceilings:
- H = 1.0 - for ceilings of 2.7 meters high.
- H = 1.05 - for rooms up to 3 meters high.
- H = 1,1 - for a room with a ceiling of up to 3.5 meters.
- H = 1.15 - up to 4 meters.
- H = 1.2 - the need for heat for a higher room.
As you can see, for rooms with high ceilings, 5% should be added to the calculation for every half meter of height, starting from 3.5 m.
By the law of nature, warm, heated air rushes up. To mix its entire volume, the heating devices will have to work hard.

The estimated role of the ceiling and floor
Not only do they lead to a decrease in the thermal power of batteries insulated external walls. The ceiling in contact with a warm room also minimizes losses in heating a room.
The coefficient "W" in the calculation formula is just in order to provide for this:
- W = 1.0 - if located at the top, for example, an unheated uninsulated attic.
- W = 0.9 - for an unheated, but insulated attic or other insulated room from above.
- W = 0.8 - if the floor above the room is heated.
The W indicator can be adjusted upwards for the premises of the first floor, if they are located on the ground, above an unheated basement or basement. Then the numbers will be as follows: the floor is insulated + 20% (x1,2); the floor is not insulated + 40% (x1.4).
Frame quality is the key to heat
Windows - once a weak spot in the insulation of living space. Modern frames with double-glazed windows have significantly improved the protection of rooms from street cold.
The degree of quality of the windows in the formula for calculating thermal power describes the coefficient "G".
The calculation is based on a standard frame with a single-chamber double-glazed window, in which the coefficient is 1.
Consider other options for applying the coefficient:
- G = 1.0 - frame with single-chamber double-glazed window.
- G = 0.85 - if the frame is equipped with a two- or three-chamber double-glazed window.
- G = 1.27 - if the window has an old wooden frame.
So, if the house has old frames, then the heat loss will be significant. Therefore, more powerful batteries will be required. Ideally, it is advisable to replace such frames, because these are additional heating costs.
Window size matters
Following the logic, it can be argued that the larger the number of windows in the room and the wider their overview, the more sensitive heat leakage through them. The coefficient "X" from the formula for calculating the thermal power required by the batteries, just reflects this.

The norm is the result of dividing the area of window openings by the area of the room equal from 0.2 to 0.3.
Here are the main values of the coefficient X for various situations:
- X = 1.0 - with a ratio of 0.2 to 0.3.
- X = 0.9 - for the area ratio from 0.1 to 0.2.
- X = 0.8 - with a ratio of up to 0.1.
- X = 1.1 - if the area ratio is from 0.3 to 0.4.
- X = 1.2 - when it is from 0.4 to 0.5.
If the footage of window openings (for example, in rooms with panoramic windows) goes beyond the proposed ratios, it is reasonable to add another 10% to the X value with an increase in the area ratio by 0.1.
The door located in the room, which is regularly used in winter to access the open balcony or loggia, makes its own amendments to the heat balance. For such a room, it will be correct to increase X by another 30% (x1.3).
Loss of thermal energy is easily compensated by a compact installation under the balcony entrance of a channel water or electric convector.
The effect of battery closure
Of course, the radiator that is less fenced by various artificial and natural obstacles will give better heat. In this case, the formula for calculating its thermal power is expanded due to the coefficient "Y", taking into account the operating conditions of the battery.
The most common location for radiators is under the windowsill. With this position, the coefficient value is 1.
Consider typical situations for placing radiators:
- Y = 1.0 - immediately under the windowsill.
- Y = 0.9 - if the battery is suddenly completely open from all sides.
- Y = 1.07 - when the radiator is blocked by a horizontal ledge of the wall
- Y = 1.12 - if the battery located under the window sill is covered by the front casing.
- Y = 1.2 - when the heater is blocked on all sides.
The shifted long blackout curtains also cause a cooling in the room.

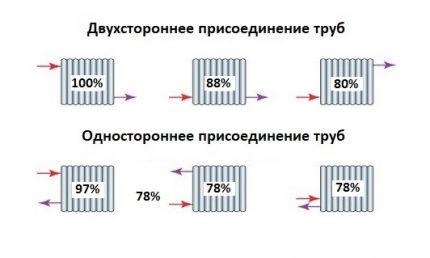
Radiator Connectivity
The efficiency of its operation directly depends on the method of connecting the radiator to the indoor heating wiring. Often, homeowners sacrifice this indicator for the sake of the beauty of the room. The formula for calculating the required heat capacity takes into account all this through the coefficient "Z".
We give the values of this indicator for various situations:
- Z = 1.0 - the inclusion of a radiator in the overall circuit of the heating system with a diagonal reception, which is the most justified.
- Z = 1.03 - Another, the most common due to the small length of the eyeliner, the option of joining "from the side."
- Z = 1.13 - The third method is “from below on two sides.” Thanks to plastic pipes, it was he who quickly took root in the new construction, despite the much lower efficiency.
- Z = 1.28 - Another, very low-efficient method "from the bottom on the one hand." It deserves consideration only because some designs of radiators are supplied with ready-made units with connection to a single point of the pipe and supply and return.
The air vents installed in them will help to increase the efficiency of heating devices, which will save the system from “airing” in a timely manner.
The principle of operation of any water heater is based on the physical properties of a hot liquid rising up, and after cooling down.
Therefore, it is strongly not recommended to use the connections of heating systems to radiators, in which the supply pipe is at the bottom and the return pipes at the top.
A practical example of calculating thermal power
Initial data:
- Corner room without a balcony on the second floor of a two-story cinder block plastered house in a calm area of Western Siberia.
- Room length 5.30 m X width 4.30 m = area 22.79 sq.m.
- Window width 1.30 m X height 1.70 m = area 2.21 sq.m.
- Room height = 2.95 m.
Calculation Sequence:
| Room area in sq.m .: | S = 22.79 |
| Window Orientation South: | R = 1,0 |
| The number of external walls is two: | K = 1,2 |
| Insulation of external walls - standard: | U = 1,0 |
| Minimum temperature - up to -35 ° C: | T = 1.3 |
| Room height - up to 3 m: | H = 1.05 |
| The room above is an uninsulated attic: | W = 1.0 |
| Frames - single-chamber double-glazed window: | G = 1.0 |
| The ratio of the area of the window and the room is up to 0.1: | X = 0.8 |
| Radiator position - under the windowsill: | Y = 1.0 |
| Radiator connection - diagonally: | Z = 1.0 |
| Total (do not forget to multiply by 100): | Q = 2 986 watts |
The following is a description of the calculation of the number of radiator sections and the required number of batteries. It is based on the obtained results of thermal capacities, taking into account the dimensions of the proposed installation sites for heating devices.
Regardless of the outcome, it is recommended that in corner rooms not only window sills be equipped with radiators. Batteries should be installed near the “blind” external walls or near the corners that are most exposed to freezing due to street cold.
Specific thermal power of battery sections
Even before performing the general calculation of the required heat transfer of heating devices, it is necessary to decide which demountable batteries of which material will be installed in the premises.
The choice should be based on the characteristics of the heating system (internal pressure, coolant temperature). At the same time, do not forget about the very varied cost of purchased products.
About how to correctly calculate the right amount of different batteries for heating, and we will go further.
At a coolant of 70 ° C, standard 500 mm sections of radiators made of dissimilar materials have unequal specific heat output “q”.
- Cast Iron - q = 160 Watts (specific power of one pig-iron section). Radiators from this metal suitable for any heating system.
- Steel - q = 85 Watts. Steel tubular radiators can work in the most severe operating conditions. Their sections are beautiful in their metallic luster, but have the least heat dissipation.
- Aluminum - q = 200 Watts. Lightweight, aesthetic aluminum radiators must be installed only in autonomous heating systems in which the pressure is less than 7 atmospheres. But in terms of heat transfer to their sections there are no equal.
- Bimetal - q = 180 watts. Insides bimetal radiators made of steel, and the heat sink surface is made of aluminum. These batteries will withstand all kinds of pressure and temperature conditions. The specific thermal power of the bimetal sections is also at altitude.
The given q values are rather arbitrary and are used for preliminary calculation. More accurate numbers are contained in the passports of the purchased heating appliances.
Calculation of the number of sections of radiators
Collapsible radiators from any material are good because in order to achieve their rated thermal power, individual sections can be added or removed.
To determine the required number of "N" battery sections from the selected material, the following formulas are used:
N = Q / q,
Where:
- Q = previously calculated required heat output of devices for heating a room,
- q = thermal power specific section of the proposed battery installation.
Having calculated the total required number of sections of radiators in the room, you need to understand how many batteries you need to install. This calculation is based on a comparison of the dimensions of the proposed locations. installation of heating appliances and battery sizes, taking into account the liner.

For preliminary calculations, you can arm with data on the width of the sections of different radiators:
- cast iron = 93 mm
- aluminum = 80 mm
- bimetallic = 82 mm.
In the manufacture of collapsible radiators from steel pipes, manufacturers do not adhere to certain standards. If you want to supply such batteries, you should approach the issue individually.
You can also use our free online calculator to calculate the number of sections:
Improving heat transfer efficiency
When the radiator heats the room’s internal air, the external wall is also intensely heated in the area behind the battery. This leads to additional unjustified heat loss.
It is proposed to improve the heat transfer efficiency of the radiator to block the heater from the outer wall with a heat-reflecting screen.
The market offers many modern insulating materials with a heat-reflecting foil surface. The foil protects the warm air warmed by the battery from contact with a cold wall and directs it into the room.
For proper operation, the boundaries of the installed reflector must exceed the dimensions of the radiator and protrude on each side by 2-3 cm. The gap between the heater and the thermal protection surface should be left at 3-5 cm.
For the manufacture of a heat-reflecting screen, isospan, penofol, alufom can be advised. A rectangle of the required dimensions is cut out of the purchased roll and fixed to the wall at the radiator installation site.
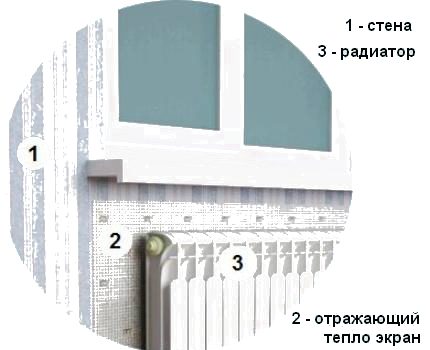
It is recommended to separate the insulation sheet from the external wall with a small air gap, for example, using a thin plastic grill.
If the reflector is joined from several parts of the insulating material, the joints on the side of the foil must be glued with metallized adhesive tape.
Conclusions and useful video on the topic
Small films will present the practical embodiment of some engineering tips in everyday life. In the next video you can see a practical example of calculating heating radiators:
The change in the number of sections of radiators is discussed in this video:
The following video tells how to mount the reflector under the battery:
The acquired skills in calculating the thermal power of different types of heating radiators will help the home foreman in the competent design of the heating system. And housewives will be able to verify the correctness of the battery installation process by third-party specialists.
Did you do your own calculating the power of heating batteries for your home? Or faced with problems arising from the installation of low-power heating devices? Tell your readers about your experience - please leave comments below.

 Installing heating batteries: do-it-yourself technology for the correct installation of radiators
Installing heating batteries: do-it-yourself technology for the correct installation of radiators  Replacing heating radiators: a guide for dismantling old batteries and installing new appliances
Replacing heating radiators: a guide for dismantling old batteries and installing new appliances  Cast-iron radiators: characteristics of batteries, their advantages and disadvantages
Cast-iron radiators: characteristics of batteries, their advantages and disadvantages  Wiring diagrams for radiators: an overview of the best ways
Wiring diagrams for radiators: an overview of the best ways  Steel heating radiators: varieties, characteristics and advantages of batteries
Steel heating radiators: varieties, characteristics and advantages of batteries  How much does it cost to connect gas to a private house: the price of organizing gas supply
How much does it cost to connect gas to a private house: the price of organizing gas supply  The best washing machines with dryer: model rating and customer tips
The best washing machines with dryer: model rating and customer tips  What is the color temperature of light and the nuances of choosing the temperature of the lamps to suit your needs
What is the color temperature of light and the nuances of choosing the temperature of the lamps to suit your needs  Replacement of a geyser in an apartment: replacement paperwork + basic norms and requirements
Replacement of a geyser in an apartment: replacement paperwork + basic norms and requirements
In our apartment in one of the rooms, the builders clearly miscalculated - the window was 2.1 meters long and the battery was 80 cm, and it starts earlier, i.e. reaches approximately the middle of the first leaflet. Accordingly, the opposite side of the window is almost always cold, especially when the wind or frost. A heat-insulating screen helps not bad, but we will do additional external insulation in the spring.
All her life she lived in houses and apartments with cast-iron radiators. They were always as wide as a window, I'm so used to it. Recently I changed the old batteries to modern appliances, and those are small, half the window, and they still assured me that this is enough for heating. Of course, the room is cold, the radiator can not cope. In the spring I will change everything. How much easier with cast-iron radiators (
Hello.Thanks for the detailed information. The formula for calculating the heat output that you include includes heating the room to what temperature? That is, the coefficients of this formula as a result allow you to find out only about heat losses in kilowatts, or does the formula (coefficients) include a reserve that will compensate for heat loss and plus provide heating of room temperature to a specific degree?