Gas consumption for heating a house 200 m²: determination of costs when using main and bottled fuel
Owners of medium and large cottages must plan the cost of maintaining housing. Therefore, the task often arises of calculating the gas consumption for heating a house 200 m2 or larger area. The original architecture usually does not allow you to use the method of analogies and find ready-made calculations.
However, there is no need to pay money to solve this problem. All calculations can be done independently. This will require knowledge of certain regulations, as well as an understanding of physics and geometry at the school level.
We will help you figure out this vital issue for a home economist. We will show you by what formulas the calculations are made, what characteristics you need to know to get the result. The article we have presented provides examples on the basis of which it will be easier to make your own calculation.
The content of the article:
Finding the value of energy loss
In order to determine the amount of energy that a house loses, it is necessary to know the climatic features of the area, the thermal conductivity of materials and ventilation rates. And in order to calculate the required volume of gas, it is enough to know its calorific value. The most important thing in this work is attention to detail.
Heating a building should compensate for the heat loss that occurs for two main reasons: heat leakage around the perimeter of the house and the influx of cold air through the ventilation system. Both of these processes are described by mathematical formulas, according to which you can independently carry out calculations.
Thermal conductivity and thermal resistance of the material
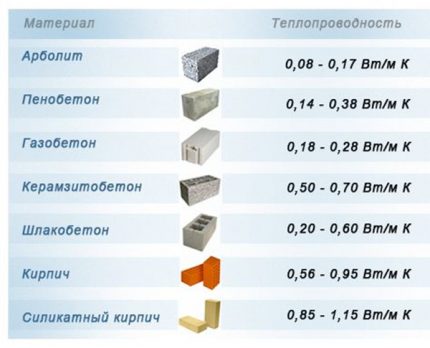
Any material can conduct heat. The intensity of its transmission is expressed through the coefficient of thermal conductivity λ (W / (m × ° C)). The lower it is, the better the structure is protected from freezing in winter.
However, buildings can be folded or insulated with materials of various thicknesses. Therefore, in practical calculations, the heat transfer resistance coefficient is used:
R (m2 × ° C / W)
It is associated with thermal conductivity by the following formula:
R = h / λ,
Where h - material thickness (m).
Example. We determine the coefficient of resistance to heat transfer of different width aerated concrete blocks of brand D700 at λ = 0.16:
- width 300 mm: R = 0.3 / 0.16 = 1.88;
- width 400 mm: R = 0.4 / 0.16 = 2.50.
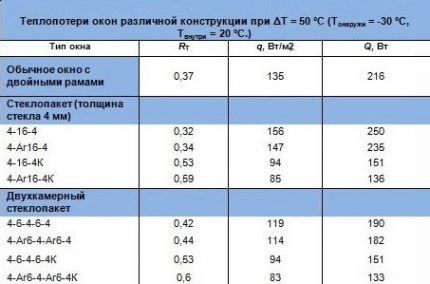
For insulation materials and window blocks can be given both the coefficient of thermal conductivity and the coefficient of resistance to heat transfer.
If the enclosing structure consists of several materials, then when determining the coefficient of resistance to heat transfer of the whole “pie”, the coefficients of its individual layers are summed.
Example. The wall is built of aerated concrete blocks (λb = 0.16), 300 mm thick. Outside it is insulated extruded polystyrene foam (λp = 0.03) 50 mm thick, and lined with lining from the inside (λv = 0.18), 20 mm thick.

Now you can calculate the total coefficient of resistance to heat transfer:
R = 0.3 / 0.16 + 0.05 / 0.03 + 0.02 / 0.18 = 1.88 + 1.66 + 0.11 = 3.65.
The contribution of layers that are insignificant in the “heat saving” parameter can be neglected.
Calculation of heat loss through building envelopes
Heat loss Q (W) through a homogeneous surface can be calculated as follows:
Q = S × dT / R,
Where:
- S - area of the considered surface (m2);
- dT - temperature difference between the air inside and outside the room (° C);
- R - surface heat transfer coefficient (m2 * ° C / W).
To determine the total indicator of all heat losses, perform the following actions:
- allocate areas that are uniform in the coefficient of resistance to heat transfer;
- calculate their area;
- determine the indicators of thermal resistance;
- calculate heat loss for each of the sites;
- summarize the obtained values.
Example. Corner room 3 × 4 meters on the top floor with a cold attic. The final ceiling height is 2.7 meters. There are 2 windows measuring 1 × 1.5 m.
We find the heat loss through the perimeter at an air temperature inside of “+25 ° С“, and outside “–15 ° С”:
- Let us single out sections that are uniform in coefficient of resistance: ceiling, wall, windows.
- Ceiling area SP = 3 × 4 = 12 m2. Window area Sabout = 2 × (1 × 1.5) = 3 m2. Wall area Swith = (3 + 4) × 2.7 – Sabout = 29.4 m2.
- The coefficient of thermal resistance of the ceiling is composed of the overlap index (board thickness of 0.025 m), insulation (mineral wool slabs 0.10 m thick) and the wooden floor of the attic (wood and plywood with a total thickness of 0.05 m): RP = 0.025 / 0.18 + 0.1 / 0.037 + 0.05 / 0.18 = 3.12. For windows, the value is taken from the passport of a two-chamber double-glazed window: Rabout = 0.50. For a wall folded as in the previous example: Rwith = 3.65.
- QP = 12 × 40 / 3.12 = 154 watts. Qabout = 3 × 40 / 0.50 = 240 watts. Qwith = 29.4 × 40 / 3.65 = 322 W.
- General heat loss of the model room through the building envelope Q = QP + Qabout + Qwith = 716 watts.
Calculation using the above formulas gives a good approximation, provided that the material meets the stated thermal conductivity and there are no errors that may be made during construction. Also a problem may be the aging of materials and the structure of the house as a whole.
Typical wall and roof geometry
The linear parameters (length and height) of the structure when determining heat losses are usually taken internal rather than external. That is, when calculating heat transfer through the material, the contact area of warm, not cold air, is taken into account.

Thus, for example, when the dimensions of the house are 8 × 10 meters and the wall thickness is 0.3 meters, the inner perimeter Pint = (9.4 + 7.4) × 2 = 33.6 m, and the outer Pout = (8 + 10) × 2 = 36 m.
The interfloor overlap usually has a thickness of 0.20 to 0.30 m. Therefore, the height of two floors from the floor of the first to the ceiling of the second from the outside will be equal to Hout = 2.7 + 0.2 + 2.7 = 5.6 m. If you add up only the finishing height, you get a lower value: Hint = 2.7 + 2.7 = 5.4 m. Interfloor overlapping, unlike walls, does not carry the function of insulation, therefore, for calculations it is necessary to take Hout.
For two-story houses with dimensions of about 200 m2 the difference between the area of the walls inside and outside is from 6 to 9%. Similarly, in terms of internal dimensions, the geometric parameters of the roof and floors are taken into account.
The calculation of the wall area for simple cottages in geometry is elementary, since the fragments consist of rectangular sections and pediments of the attic and attic rooms.
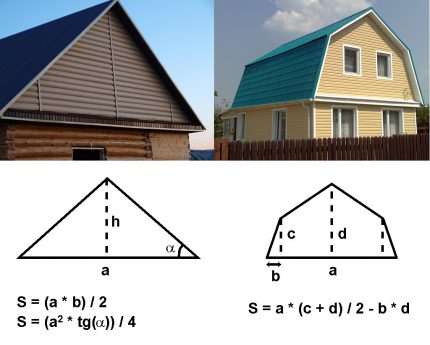
When calculating heat loss through the roof in most cases, it is enough to apply formulas to find the areas of a triangle, rectangle and trapezoid.
The area of the laid roof cannot be taken when determining heat losses, since it also goes to overhangs that are not taken into account in the formula. In addition, often the material (for example, roofing or profiled galvanized sheet) is placed with a slight overlap.

The rectangular geometry of the windows also does not cause problems in the calculations. If the double-glazed windows have a complex shape, then their area can not be calculated, but learned from the product passport.
Heat loss through the floor and foundation
The calculation of heat loss to the soil through the floor of the lower floor, as well as through the walls and floor of the basement, is considered according to the rules prescribed in Appendix “E” SP 50.13330.2012. The fact is that the rate of heat propagation in the earth is much lower than in the atmosphere, therefore, soils can also be conditionally attributed to insulation material.
But since they are characterized by freezing, the floor is divided into 4 zones. The width of the first three is 2 meters, and the remainder is referred to the fourth.
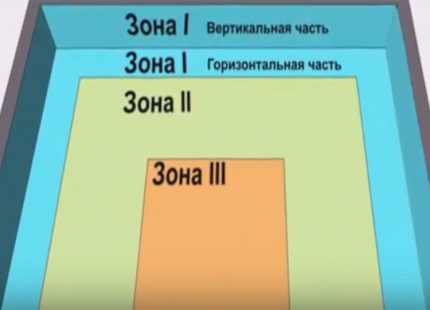
For each zone, determine the coefficient of resistance to heat transfer, which adds soil:
- zone 1: R1 = 2.1;
- zone 2: R2 = 4.3;
- zone 3: R3 = 8.6;
- zone 4: R4 = 14.2.
If the floors are insulated, then to determine the total coefficient of thermal resistance add up the indicators of insulation and soil.
Example. Suppose that a house with external dimensions of 10 × 8 m and a wall thickness of 0.3 meters has a basement with a depth of 2.7 meters. Its ceiling is located at ground level. It is necessary to calculate the heat loss to the soil at an internal air temperature of “+25 ° C” and an external temperature of “–15 ° C”.
Let the walls be made of FBS blocks 40 cm thick (λf = 1.69). Inside, they are trimmed with a board 4 cm thick (λd = 0.18). The basement floor is poured with expanded clay concrete, 12 cm thick (λto = 0.70). Then the coefficient of thermal resistance of the walls of the basement: Rwith = 0.4 / 1.69 + 0.04 / 0.18 = 0.46, and the floor RP = 0.12 / 0.70 = 0.17.
The internal dimensions of the house will be 9.4 × 7.4 meters.
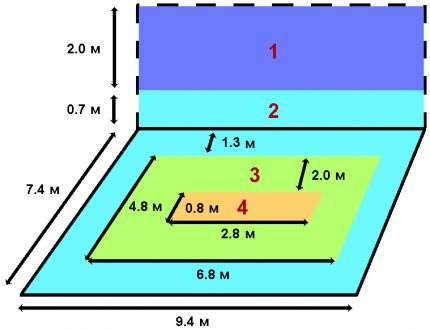
We calculate the areas and coefficients of resistance to heat transfer by zones:
- Zone 1 runs only along the wall. It has a perimeter of 33.6 m and a height of 2 m. Therefore S1 = 33.6 × 2 = 67.2. Rs1 = Rwith + R1 = 0.46 + 2.1 = 2.56.
- Zone 2 on the wall. It has a perimeter of 33.6 m and a height of 0.7 m. Therefore S2c = 33.6 × 0.7 = 23.52. Rz2s = Rwith + R2 = 0.46 + 4.3 = 4.76.
- Zone 2 on the floor. S2p = 9.4 × 7.4 – 6.8 × 4.8 = 36.92. Rz2p = RP + R2 = 0.17 + 4.3 = 4.47.
- Zone 3 is only on the floor. S3 = 6.8 × 4.8 – 2.8 × 0.8 = 30.4. Rh3 = RP + R3 = 0.17 + 8.6 = 8.77.
- Zone 4 is only on the floor. S4 = 2.8 × 0.8 = 2.24. Rs4 = RP + R4 = 0.17 + 14.2 = 14.37.
Ground floor heat loss Q = (S1 / Rs1 + S2c / Rz2s + S2p / Rz2p + S3 / Rh3 + S4 / Rs4) × dT = (26.25 + 4.94 + 8.26 + 3.47 + 0.16) × 40 = 1723 W.
Accounting for unheated premises
Often when calculating heat loss, a situation arises when the house has an unheated, but insulated room. In this case, energy transfer occurs in two stages. Consider this situation in the attic.
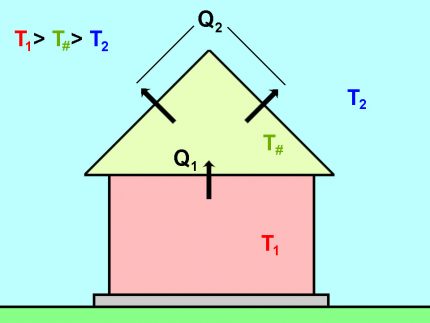
The main problem is that the area of overlap between the attic and the upper floor is different from the area of the roof and gables. In this case, it is necessary to use the condition of heat transfer balance Q1 = Q2.
It can also be written in the following way:
K1 × (T1 - T#) = K2 × (T# - T2),
Where:
- K1 = S1 / R1 + … + Sn / Rn for overlapping between the warm part of the house and the cold room;
- K2 = S1 / R1 + … + Sn / Rn for overlapping between a cold room and the street.
From the equality of heat transfer, we find the temperature that will be established in a cold room with known values in the house and on the street. T# = (K1 × T1 + K2 × T2) / (K1 + K2) After that, we substitute the value in the formula and find the heat loss.
Example. Let the internal size of the house is 8 x 10 meters. The roof angle is 30 °. The air temperature in the rooms is “+25 ° С”, and outside “–15 ° С”.
The coefficient of thermal resistance of the ceiling is calculated as in the example given in the section for calculating heat losses through building envelopes: RP = 3.65. The overlap area is 80 m2, so K1 = 80 / 3.65 = 21.92.
Roof area S1 = (10 × 8) / cos(30) = 92.38. We consider the coefficient of thermal resistance, taking into account the thickness of the tree (crate and finish - 50 mm) and mineral wool (10 cm): R1 = 2.98.
Window area for pediment S2 = 1.5. For an ordinary two-chamber double-glazed window thermal resistance R2 = 0.4. The area of the pediment is calculated by the formula: S3 = 82 × tg(30) / 4 – S2 = 7.74. The coefficient of resistance to heat transfer is the same as that of the roof: R3 = 2.98.
We calculate the coefficient for the roof (not forgetting that the number of pediments is two):
K2 = S1 / R1 + 2 × (S2 / R2 + S3 / R3) = 92.38 / 2.98 + 2 × (1.5 / 0.4 + 7.74 / 2.98) = 43.69.
We calculate the air temperature in the attic:
T# = (21.92 × 25 + 43.69 × (–15)) / (21.92 + 43.69) = –1.64 ° С.
We substitute the obtained value into any of the formulas for calculating heat losses (if they are balanced, they are equal) and we obtain the desired result:
Q1 = K1 × (T1 – T#) = 21.92 × (25 - (–1.64)) = 584 W.
Ventilation cooling
A ventilation system is installed to maintain a normal microclimate in the house. This leads to an influx of cold air into the room, which also must be taken into account when calculating heat loss.
Requirements for the volume of ventilation are spelled out in several regulatory documents. When designing an intra-house cottage system, first of all, it is necessary to take into account the requirements of §7 SNiP 41-01-2003 and §4 SanPiN 2.1.2.2645-10.
Since watt is the generally accepted unit for measuring heat loss, the heat capacity of air c (kJ / kg × ° C) must be reduced to the dimension “W × h / kg × ° C”. For air at sea level, you can take the value c = 0.28 W × h / kg × ° C.
Since the ventilation volume is measured in cubic meters per hour, it is also necessary to know the air density q (kg / m3) At normal atmospheric pressure and average humidity, this value can be taken q = 1.30 kg / m3.

The energy consumption for the compensation of heat losses due to ventilation can be calculated using the following formula:
Q = L × q × c × dT = 0.364 × L × dT,
Where:
- L - air consumption (m3 / h);
- dT - temperature difference between room and incoming air (° C).
If cold air enters the house directly, then:
dT = T1 - T2,
Where:
- T1 - indoor temperature;
- T2 - temperature outside.
But for large objects in the ventilation system usually integrate recuperator (heat exchanger). It can significantly save energy, as the partial heating of the incoming air occurs due to the temperature of the outlet stream.
The effectiveness of such devices is measured in their efficiency k (%). In this case, the previous formula will take the form:
dT = (T1 - T2) × (1 - k / 100).
Gas flow calculation
Knowing total heat loss, you can simply calculate the required consumption of natural or liquefied gas for heating a house with an area of 200 m2.
The amount of energy released, in addition to the volume of fuel, is affected by its calorific value. For gas, this indicator depends on the humidity and chemical composition of the supplied mixture. Distinguish the highest (Hh) and lower (Hl) calorific value.

To calculate the amount of fuel that is guaranteed to be sufficient for heating, the lower calorific value, which can be obtained from the gas supplier, is substituted into the formula. The standard unit of calorific value is “mJ / m3”Or“ mJ / kg ”. But since the units of measure and power of the boilers and heat losses operate with watts, not joules, it is necessary to perform the conversion, given that 1 mJ = 278 W × h.
If the value of the lower calorific value of the mixture is unknown, then it is permissible to take the following averaged figures:
- for natural gas Hl = 9.3 kW × h / m3;
- for liquefied gas Hl = 12.6 kW × h / kg.
Another indicator necessary for calculations is the boiler efficiency K. Usually it is measured in percent. The final formula for gas flow over a period of time E (h) has the following form:
V = Q × E / (Hl × K / 100).
The period when centralized heating in houses is turned on is determined by the average daily air temperature.
If over the past five days it has not exceeded “+ 8 ° С”, then according to the Decree of the Government of the Russian Federation No. 307 dated 05/13/2006, heat supply to the house must be provided. For private homes with autonomous heating, these figures are also used when calculating fuel consumption.
The exact data on the number of days with a temperature not higher than “+ 8 ° С” for the area where the cottage is built can be found in the local branch of the Hydrometeorological Center.
If the house is located close to a large settlement, then it is easier to use the table. 1. SNiP 23-01-99 (column No. 11). Multiplying this value by 24 (hours per day) we get the parameter E from the equation for calculating gas flow.
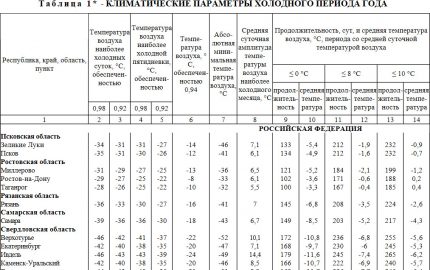
If the volume of air inflow and the temperature inside the rooms are constant (or with slight fluctuations), then the heat loss through the building envelope and due to the ventilation of the rooms will be directly proportional to the outdoor temperature.
Therefore per parameter T2 in the equations for calculating heat loss, you can take the value from column No. 12 of the table. 1. SNiP 23-01-99.
Example for a 200 m cottage2
We calculate the gas consumption for a cottage near the city of Rostov-on-Don. Duration of heating period: E = 171 × 24 = 4104 h. Average street temperature T2 = - 0.6 ° C. Desired temperature in the house: T1 = 24 ° C.
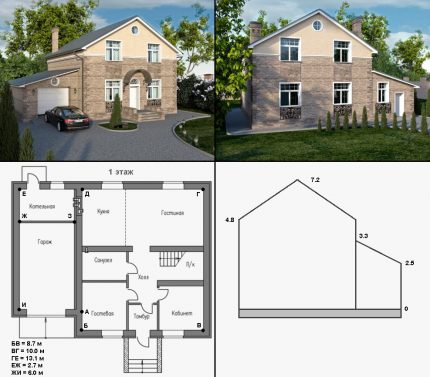
Step 1. We calculate the heat loss through the perimeter without taking into account the garage.
To do this, select homogeneous sections:
- Window. In total there are 9 windows 1.6 × 1.8 m in size, one window 1.0 × 1.8 m in size and 2.5 round windows 0.38 m in size2 each one. Total window area: Swindow = 28.60 m2. According to the passport of products Rwindow = 0.55. Then Qwindow = 1279 watts.
- Doors There are 2 insulated doors measuring 0.9 x 2.0 m. Their area: Sthe door = 3.6 m2. According to the product passport Rthe door = 1.45. Then Qthe door = 61 watts.
- Blank wall. Section “ABVGD”: 36.1 × 4.8 = 173.28 m2. Plot “YES”: 8.7 × 1.5 = 13.05 m2. Plot “DEJ”: 18.06 m2. The area of the roof gable: 8.7 × 5.4 / 2 = 23.49. Total blank wall area: Swall = 251.37 – Swindow – Sthe door = 219.17 m2. The walls are made of aerated concrete 40 cm thick and hollow facing bricks. Rwalls = 2.50 + 0.63 = 3.13. Then Qwalls = 1723 W.
Total heat loss through the perimeter:
Qperim = Qwindow + Qthe door + Qwalls = 3063 watts
Step 2 We calculate the heat loss through the roof.
The insulation is a continuous crate (35 mm), mineral wool (10 cm) and lining (15 mm). Rthe roof = 2.98. Roof area above the main building: 2 × 10 × 5.55 = 111 m2and above the boiler room: 2.7 × 4.47 = 12.07 m2. Total Sthe roof = 123.07 m2. Then Qthe roof = 1016 watts.
Step 3 Calculate heat loss through the floor.
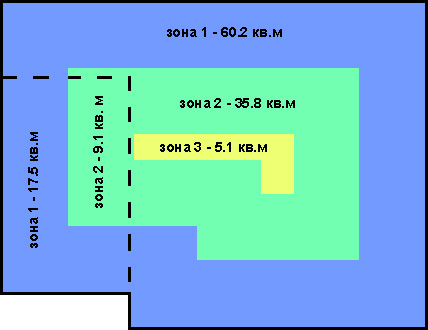
Resistance to heat transfer is provided by the boards of the rough flooring and plywood under the laminate (5 cm in total), as well as basalt insulation (5 cm). Rgender = 1.72. Then the heat loss through the floor will be equal to:
Qfloor = (S1 / (Rfloor + 2.1) + S2 / (Rfloor + 4.3) + S3 / (Rfloor + 2.1)) × dT = 546 watts.
Step 4 We calculate the heat loss through a cold garage. Its floor is not insulated.
From a heated house, heat penetrates in two ways:
- Through the bearing wall. S1 = 28.71, R1 = 3.13.
- Through a brick wall with a boiler room. S2 = 11.31, R2 = 0.89.
We get K1 = S1 / R1 + S2 / R2 = 21.88.
From the garage, the heat goes out as follows:
- Through the window. S1 = 0.38, R1 = 0.55.
- Through the gate. S2 = 6.25, R2 = 1.05.
- Through the wall. S3 = 19.68, R3 = 3.13.
- Through the roof. S4 = 23.89, R4 = 2.98.
- Across the floor. Zone 1. S5 = 17.50, R5 = 2.1.
- Across the floor. Zone 2. S6 = 9.10, R6 = 4.3.
We get K2 = S1 / R1 + … + S6 / R6 = 31.40
We calculate the temperature in the garage, subject to the balance of heat transfer: T# = 9.2 ° C. Then the heat loss will be equal to: Qgarage = 324 watts.
Step 5 We calculate the heat loss due to ventilation.
Let the calculated ventilation volume for such a cottage with 6 people staying there be 440 m3/hour. A recuperator with an efficiency of 50% is installed in the system. Under these conditions, heat loss: Qvent = 1970 watts
Step. 6. We determine the total heat loss by adding all the local values: Q = 6919 watts
Step 7 We calculate the amount of gas needed to heat the model house in the winter with a boiler efficiency of 92%:
- Natural gas. V = 3319 m3.
- Liquefied gas. V = 2450 kg.
After calculations, you can analyze the financial costs of heating and the feasibility of investments aimed at reducing heat loss.
Conclusions and useful video on the topic
Thermal conductivity and heat transfer resistance of materials. Calculation rules for walls, roof and floor:
The most difficult part of the calculations to determine the volume of gas needed for heating is finding the heat loss of the heated object. Here, first of all, you need to carefully consider geometric calculations.
If the financial costs of heating seem excessive, then you should think about additional insulation of the house. Moreover, calculations of heat loss show well the freezing structure.
Please leave comments in the block below, ask questions on unclear and interesting points, post a photo on the topic of the article. Share your own experience in making calculations to find out the cost of heating. It is possible that your advice will greatly help site visitors.

 The average gas consumption for heating a house is 150 m²: an example of calculations and an overview of heat engineering formulas
The average gas consumption for heating a house is 150 m²: an example of calculations and an overview of heat engineering formulas  Gas consumption for heating a house 100 m²: calculation features for liquefied and natural gas + examples with formulas
Gas consumption for heating a house 100 m²: calculation features for liquefied and natural gas + examples with formulas  How to calculate gas consumption for heating a house in accordance with the norms
How to calculate gas consumption for heating a house in accordance with the norms  Types of heating a country house: a comparison of heating systems by type of fuel
Types of heating a country house: a comparison of heating systems by type of fuel  Calculation of the heating system of a private house: rules and examples of calculation
Calculation of the heating system of a private house: rules and examples of calculation  How to arrange heating of a private house with your own hands: schemes for organizing an autonomous heating system
How to arrange heating of a private house with your own hands: schemes for organizing an autonomous heating system  How much does it cost to connect gas to a private house: the price of organizing gas supply
How much does it cost to connect gas to a private house: the price of organizing gas supply  The best washing machines with dryer: model rating and customer tips
The best washing machines with dryer: model rating and customer tips  What is the color temperature of light and the nuances of choosing the temperature of the lamps to suit your needs
What is the color temperature of light and the nuances of choosing the temperature of the lamps to suit your needs  Replacement of a geyser in an apartment: replacement paperwork + basic norms and requirements
Replacement of a geyser in an apartment: replacement paperwork + basic norms and requirements